Tesla Cybertruck vs Ford Pinto: Which is the Bigger Fire-Trap?

A couple recent news reports said the Tesla Cybertruck caught fire and killed people more often than the infamous Ford Pinto of the 1970s. Let’s look statistically at the data and see if this is believable. Surely we’ve learned from past experiences with corporate misfeasance, not to mention fire safety?

Car Safety Issues: Historical & Modern

The Ford Pinto is a storied automobile ^[1], to say the least. It was a first reaction from Ford to smaller imported cars, and it set the tone for some pretty despicable behavior by American automakers: general incompetence, stubborn refusal to understand customer needs for fuel efficiency, and in this case criminal neglect of safety resulting in multiple deaths.

It had the regrettable tendency, upon even mild impact from behind, to burst the fuel tank and spray fuel over hot parts and into the back seat. Worse, this problem was understood at Ford, and largely ignored:

Ford was aware of the Pinto’s propensity to catch fire. Early crash tests, performed in anticipation of a proposed safety standard regarding rear-end collisions and fuel leakage, showed the Pinto was prone to fuel leakage and fire in low-speed, rear-end impacts. Ford considered several fixes, including a shield behind the axle and a rubberized bladder for the fuel tank, but rejected these as they would have added cost and put the program behind schedule.

According to The Unknown Iacocca, 117 lawsuits were brought against Ford for Pinto-related injuries or deaths. There is no record of how much Ford paid out, though in the case of Richard Grimshaw, Lilly Gray’s 13-year-old passenger, in 1978 the jury awarded him \$2.8 million in compensatory damages (\$13.3 million in 2024 dollars) and \$125 million (\$595 million in 2024) in punitive damages, the latter reduced to \$3.5 million (\$16.7 million) by the judge. After that verdict, Ford settled most of the rest of the Pinto cases out of court.

In 1979, the state of Indiana indicted Ford on three counts of reckless homicide after a fiery Pinto wreck killed three teenagers. This was the first time a corporation faced criminal charges for a defective product. Ford was acquitted.

Read that carefully: criminal charges. This is not just an engineering bungle. There was an infamous “Pinto Memo” obtained by litigants that showed Ford was aware of multiple safety problems, and weighed the cost of fixing them versus the cost of paying off lawsuits, including wrongful death lawsuits. Ford had to be compelled legally, kicking and screaming all the way, into making the Pinto at least somewhat safer.

If you think the cost of a wrongful death lawsuit is an accounting problem, you have committed a serious category error. This is not about accounting, or even about money. It is a moral calculation, which you have failed due to a sociopathic devotion to money.

If you’ve ever wondered why people hate CEOs and billionaires, this is why.

Tesla’s Cybertruck, of course, has its own safety concerns ^[2]:

The tacky EVs have been a source of controversy for just about everyone, owing to their apparent lack of crumple zones, hazardous self-driving software, batteries that catch fire, and a small problem where the things brick in the middle of the highway – and that’s just a tiny sampling of the many issues reported with Musk’s cyberpunk fantasy car.

Case in point, they’ve been impounded whenever they’ve shown up in the UK, and EU safety organizations are hoping to ban the things from European streets.

Fires, Specifically

An article at Fuel Arc reports the rates of fatalities in fires in Ford Pintos and Tesla Cybertrucks. ^[3]

The fatality data is relatively straightforward to acquire since death tends to leave a paper trail. They’ve gone with the lowest, most solidly verifiable numbers of deaths here in both cases. However, the number of units manufactured is more difficult to know, in a way that wasn’t obvious to me:

• Ford’s Pinto was a long(ish) time ago, so everything is kind of buried. However, they offer their thanks in an amusing way:

  Thank you, unpaid Wikipedia editors, for your oddly intense attention to detail!

• Tesla, on the other hand, treats their production numbers as super-secret. I’m a bit surprised that a public company can conceal such relevant data from their stockholders! However, there are Tesla enthusiasts who carefully keep track via a number of techniques almost like industrial espionage, and have famously accurate numbers. So that’s what’s used here.

Let’s get the numbers in to an R dataframe for analysis:

> tbl <- data.frame(TotalUnits = c(34438, 3173491), ReportedFireFatalities = c(5, 27), row.names = c("TeslaCybertruck", "FordPinto")); tbl
                TotalUnits ReportedFireFatalities
TeslaCybertruck      34438                      5
FordPinto          3173491                     27

I’m not so sure about the 7-figure accuracy in the Pinto numbers, but we just need things to be in the generally correct neighborhood, anyway.

We need to normalize the death counts somehow; ideally we’d use something like passenger-hours. That being unavailable, we’ll use the number of units produced and assume people use their cars about the same number of hours. (That could be quite a stretch between 1970 and 2020!)

Our first rough estimate of the probability of a fire death is:

That certainly looks bad, being 17 times larger than the most famous deathtrap fire in US automotive history! But is it statistically significant, and is the effect size large, on an objective basis?

To answer this, we’ll first apply the Fisher Exact Test, to tell us if the rows in the table look very different after being scaled to about the same size:

> fisher.test(tbl)

	Fisher's Exact Test for Count Data

data:  tbl
p-value = 2.255e-05
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  5.131407 44.968030
sample estimates:
odds ratio 
  17.06523 

This gets us a $p$-value of $p \sim 2.26 \times 10^{-5}$, which is very statistically significant. The effect is real, i.e., we we should believe the difference in probabilities will reproduce going forward if the cars are left unchanged.

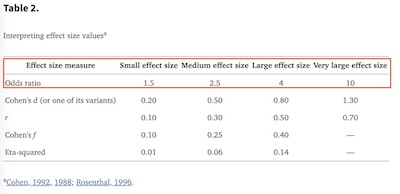The odds ratio of 17.07 is a measure of the strength of effect: an odds ratio of 1 means they’re comparable, and an odds ratio greater than one points to more fire deaths in Cybertrucks. It has confidence limits from 5.13 to 44.97. That is to say, it is very probably bounded away from 1.

Common guidelines ^{[4, especially Table 2, shown here]} say this is well beyond a “very large effect size”, in fact what we may term a “honkin’ big effect size”.

As a cross-check, we’ll also perform a test of proportion, using methods of Wilson & Newcombe. This has the satisfying interpretation of working directly on the probabilities we calculated above, and asking if they’re different:

> ptst <- prop.test(x = tbl$"ReportedFireFatalities", n = tbl$"TotalUnits"); ptst

	2-sample test for equality of proportions with continuity correction

data:  tbl$ReportedFireFatalities out of tbl$TotalUnits
X-squared = 50.837, df = 1, p-value = 1.004e-12
alternative hypothesis: two.sided
95 percent confidence interval:
 -5.28810e-06  2.78649e-04
sample estimates:
      prop 1       prop 2 
1.451885e-04 8.507981e-06 

Indeed, the result is deeply significant at $p \sim 1.00 \times 10^{-12}$.

Note that the more subtly computed, continuity-corrected probabilities computed here (“prop 1” and “prop 2”) agree almost exactly with the cruder computations above. Also, we can recover the odds ratio (odds recall, are $p/(1-p)$, so we’re taking the ratio of that between the 2 cases):

> ptst$"estimate"[["prop 1"]]/(1 - ptst$"estimate"[["prop 1"]]) * (1 - ptst$"estimate"[["prop 2"]])/ptst$"estimate"[["prop 2"]]
[1] 17.06731

So we have another vote for extreme statistical significance and agree with the Fisher exact test about the very large effect size.

The Weekend Conclusion

Look, it’s inescapable: the Cybertruck is a greater danger of fire death than the infamous Ford Pinto:

• There is no doubt the effect is real.
• There is no doubt the effect is large.

The last time this happened (the Pinto) there were regulations, there were criminal cases, and the cars were forcibly changed against the will of the manufacturer. Will we do the same against today’s New Gilded Age billionaires?

If not, I suppose tumbrels are always a possibility.

For her trouble, Kay Leadfoot received death threats in response to her article:

We got our first bonafide death threat over this coverage. Ha, I called it. Here it is in full, since it is now part of the story… less the IP address:

“You guys are a lying piece of [redacted] rag that purposely spreading false information about cybertruck .. which by will be the best selling truck in the world —- go eat [6 swear words in a row, all redacted] You purposely skewed data to make it sound bad just for your purpose of hurting Tesla. Get ready we plan on suing your [redacted]. You don’t know who we are, but we’re coming after you. go suck a tailpipe get your quickest way out.”

For the record, we do not skew any data for any purpose. We cover the news here. It’s honest work and we’ll keep getting it done.

Yeah, that tracks: the violence at the root of fascism, defending a deadly product by issuing death threats those who tell the truth.

(Ceterum censeo, Trump incarcerandam esse.)

Notes & References

1: A Gold, “The History (and Tragedy) of the Ford Pinto: Everything You Need to Know”, Motor Trend,2024-Apr-04. ↩

2: J Wilkins, “The Cybertruck Appears to Be More Deadly Than the Infamous Ford Pinto, According to a New Analysis”, The Byte, 2025-Feb-08. ↩

3: K Leadfoot, “It’s Official: the Cybertruck is More Explosive than the Ford Pinto”, Fuel Arc, 2025-Feb-06.

We assume, with great hope, that “Leadfoot” is a pseudonym. Given the death threats she has received from Musk fans, this is as understandable as it is regrettable. ↩

4: JM Maher, et al., “The Other Half of the Story: Effect Size Analysis in Quantitative Research”, CBE Life Sci Educ 12:3, 2013-Fall, pp. 345-351. DOI: 10.1187/cbe.13-04-0082. PMID: 24006382. PMC: PMC3763001.

See, in particular, Table 2. ↩